To calculate result you have to disable your ad blocker first.

Absolute Value: An Introduction With Its Properties and Examples

Table of Content
In the 19th century, the concept of absolute value evolved from its ancient Greek roots to its modern form. Although its origins date back to the distant past, the modern understanding of absolute value also emerged during this period.
The German mathematician Karl Weierstrass is credited with formalizing the concept of the modulus function in 1841. The modulus function is defined as the distance of a number from zero on a number line, without regard to its sign.
The term "absolute value" was coined by the French mathematician Augustin-Louis Cauchy in the 19th century. He used the term "Valeur Absolue" to refer to the modulus function, which became known as the absolute value in English.
In this article, we will discuss the concept of absolute value and the properties of absolute value and solve a few practice questions to enhance your comprehension.
Introduction of absolute value
On the number line, the sign of the number depends upon how far the number is from zero. If a number is positive, then its absolute value is the number itself, but if the number is negative, then its absolute value is equal to the number multiplied by -1.
For example:
The absolute value for both 5 and -5 is always 5.
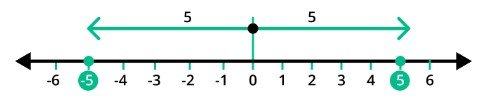
Representation of absolute value:
The modulus symbol ('| |') with the numbers between it is used to symbolize the absolute value sign. For instance, the number four is denoted by |4| in terms of absolute value.
Any number's absolute value is determined by how far it is from the line's origin. Additionally, it indicates whether a number is positive or negative and its polarity. It can never be negative since it represents distance, which cannot be negative.
Example:
The number |-9| is written as 9 in terms of modulus value.

Properties of absolute value:
The following are some important properties of modulus value:
- Let a be absolute value then
|a| ≥ - Every number is symmetric around zero, and the counterpart of negative and positive numbers is equal in the case of absolute value I.e.,
|-a| = |a| - In the absolute value case, the sum of two numbers is less or equal to the sum of individuals i.e.,
|a + b| ≤ |a| + |b| - In the product case, both absolute and individuals are equal i.e.,
|a . b| = |a| . |b| - Zero is a special number that is neither positive nor negative so
|0| = 0. - |a| = b if and only if
a = b or a = -b. - |a| < b if and only if
-b < a < b. - |a|< b if and only if
-a < -b or a > b.
How to define a function in terms of absolute value?
The absolute value function is defined as f(x) = x, where x is equal to x if x is greater than or equal to zero and -x if x is less than zero. By definition, the absolute value function always returns a non-negative value because it represents the distance between the number and zero on the number line. Therefore, let a be the absolute value then a > 0. The graph of f(x) = x looks like this:
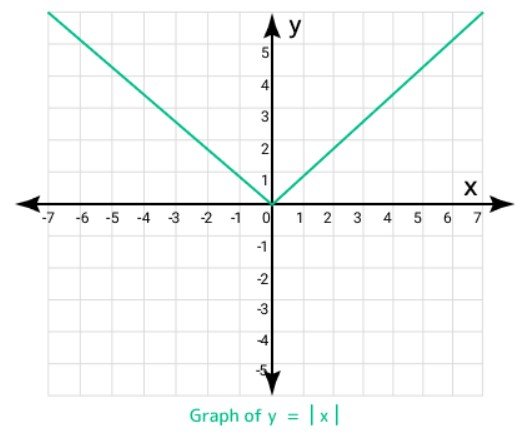
The absolute value of x, denoted by x is defined by x as defined by the absolute value function, i.e., H. x = x if x is nonnegative and x = -x if x is negative. Similarly, the square of x can be expressed as x squared = x squared because x is always non-negative.
The absolute value of zero
Positive and negative figures' absolute values have been covered. Zero's absolute value is simply zero since it has neither a positive nor a negative sign. This is so because zero is formerly zero and a number's absolute value indicates how far it's from zero on the number line. As a result, we may infer that zero's absolute value is also zero.
Examples of Absolute Value
For a better understanding of how absolute value is calculated, here are a few examples:
Example 1:
Solve the modulus value:
|-7/13||0||-0.88|
Solution:
We know that the modulus value is non-negative, so
|-7/13| = 7 / 13
|-0.88| = 0.88
We also discussed the properties of absolute value that the modulus of zero is also zero, so
|0| = 0
Example 2:
By using the definition of absolute value, find the following:
|-13||11/2||5|
Solution:
We know that the modulus value is non-negative, so
|-13| = 13
|11/2| = 11/2
|5| = 5
Example 3:
Solve for “x”
|x + 5| = 2
Solution:
Step 1: Solve modulus first
|x + 5| = 2
X + 5 = ±2
Step 2: Separate variable
X = ±2 – 5
Step 3: Separate into two cases
Case 1:
X = 2 – 5
X = -3
Case 2:
X = 2 + 5
X = 7
Step 4: Required solution set
{-3, 7}
Wrap Up
In this article, we analyzed the basic concept of absolute value more about the history of the invention of modulus value. We discussed the representation of absolute value, its properties, the modulus value of zero, and a function. We also discussed some important fields in which absolute value is useful.
