Introduction to Summation Notation: Definition, Formula, Rules, and Calculations

Summation notation, often referred to as sigma notation, is a powerful mathematical tool that allows for the representation and manipulation of a sum of a series of terms in a concise and efficient manner. Widely used in disciplines such as mathematics, physics, engineering, and computer science, summation notation simplifies complex calculations and improves the communication of mathematical ideas. 

This article delves into the world of summation notation, covering its definition, rules, properties, solved examples, and frequently asked questions.

What is Summation Notation?

Summation notation is a symbolic method for representing the sum of a sequence of numbers or mathematical expressions. It employs the Greek letter sigma (Σ) to denote the concept of sum, allowing for the short representation of a long series of numbers and making it easier to carry out complex calculations.

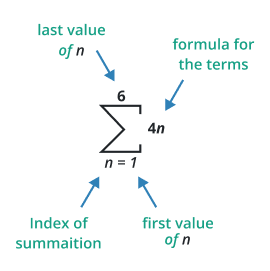
Dissecting the summation notation formula:

 let's delve into its components and the process of evaluating a summation.

Index Variable:

The index variable, typically represented by 'n' or 'i', is an integer that serves as the counter for the summation process. It takes on values from the starting point to the stopping point within the range specified.

Starting Point:

The starting point is the lower limit of the index variable. It denotes the first value the index variable will take in the summation process. For example, in the notation ∑(n=1 to N), the starting point is n=1.

Stopping Point:

The stopping point, or upper limit, indicates the last value of the index variable for which the summation will be evaluated. In the example ∑(n=1 to N), the stopping point is N.

Expression:

The expression represents the terms being summed, typically written as a function of the index variable (n). For example, in the notation ∑(n=1 to N) (a(n)), the expression is (a(n)).

Now, let's go through a simple example of evaluating a summation using Sigma notation:

Consider the summation ∑(n=1 to 4) (n^2), which represents the sum of the squares of the first four positive integers.

To evaluate this summation, we will substitute each value of the index variable (n) from the starting point (1) to the stopping point (4, inclusive) into the expression (n^2) and sum the resulting terms:

= (1^2) + (2^2) + (3^2) + (4^2)

= 1 + 4 + 9 + 16

= 30

More examples are provided at the end of the article. You can use a summation notation calculator to solve any problem. 

Rules:

Several fundamental rules apply to summation notation:

Linearity: This rule states that the summation of the sum of functions is equivalent to the sum of the summations of each individual function:

Σ (f(i) + g(i)) = Σ f(i) + Σ g(i)

Scalar Multiplication: According to this rule, the summation of a constant multiplied by a function is equal to the constant multiplied by the summation of the function:

Σ (c * f(i)) = c * Σ f(i)

Order of Operations: Summation notation abides by the order of operations, meaning that calculations within the summation notation must be executed first.

Change of Variables: A change of variables within the summation does not affect the result as long as the limits of summation are adjusted accordingly:

Σ (from i = a to b) f(i) = Σ (from j = c to d) f(j), where j = i + k for some constant k.

Properties

Summation notation is characterized by various properties, including:

Commutative Property: This property describes that the order of terms within the summation does not impact the sum:

Σ (from i = a to b) f(i) = Σ (from i = b to a) f(i)

Telescoping Property: In a series containing canceling terms, the sum can be simplified to include only the non-canceling terms.

Distributive Property: This property states that a summation can be distributed across a product of a constant and a function:

Σ (c * f(i)) = c * Σ f(i)

Solved Examples

Example 1: Sum of the first n odd numbers.

Problem: Find the sum of the first n odd numbers using summation notation.

Solution:

Odd numbers follow the sequence: 1, 3, 5, 7, …

The general form of an odd number can be expressed as 2i - 1, where “i” starts from 1. So, the sum of the first n odd numbers can be written as:

Σ (from i = 1 to n) (2i - 1)

Apply the linearity property of summation to break this into two separate sums:

Σ (from i = 1 to n) 2i - Σ (from i = 1 to n) 1

Now use the rules of scalar multiplication and linearity:

2 * Σ (from i = 1 to n) i - Σ (from i = 1 to n) 1

To solve these sums, use the formula for the sum of integers from 1 to n and the sum of a constant:

The sum of integers from 1 to n: Σ (from i = 1 to n) i = n * (n + 1) / 2

Sum of a constant: Σ (from i = 1 to n) 1 = n

So, the sum of the first n odd numbers is:

2 * (n * (n + 1) / 2) - n = n^2

Example 2: Sum of a finite arithmetic series

Problem: Find the sum of the following arithmetic series: 4 + 7 + 10 + ... + 49

Solution:

First, identify the common difference (d) and the number of terms (n) in the arithmetic series.

The common difference, d, is 3 (7 - 4 = 3).

To find the number of terms, we need to know the last term. The last term (L) is 49.

Use the formula for the nth term of an arithmetic series:

nth term = a + (n - 1)d

49 = 4 + (n - 1)3

49 = 4 + 3n - 3

48 = 3n

n = 16

Now that we have the number of terms (n = 16), find the sum using the arithmetic series formula:

Sum = n * (a + L) / 2

Sum = 16 * (4 + 49) / 2

Sum = 16 * 53 / 2

Sum = 424

So, the sum of the given arithmetic series is 424.

Example 3: Sum of an infinite geometric series

Problem: Find the sum of the following infinite geometric series: 1/2 + 1/4 + 1/8 + ...

Solution:

We need to identify the first term (a) and the common ratio (r) of the geometric series.

a = 1/2

r = 1/4 / 1/2 = 1/2

Since the common ratio r is between -1 and 1, the series converges. We can find the sum using the formula for the sum of an infinite geometric series:

Sum = a / (1 - r)

Sum = (1/2) / (1 - 1/2)

Sum = (1/2) / (1/2)

Sum = 1

Thus, the sum of the given infinite geometric series is 1.

FAQs

Q1: What is the summation symbol called?

A: The summation symbol is called sigma (Σ). It is an uppercase Greek letter used in mathematics to represent the concept of summing a series of terms.

Q2: How do you find the sum of a series using summation notation?

A: To find the sum of a series using summation notation, you need to identify the function that represents the sequence and the limits of summation. Then, apply the summation rules and properties to calculate the sum.

Q: Can summation notation be used for infinite series?

A: Yes, summation notation can be employed for infinite series. In such cases, the upper limit of summation is represented by infinity (∞). However, not all infinite series possess a finite sum. 

To determine whether an infinite series converges to a finite value, one must carefully analyze the series and apply appropriate convergence tests.

Q: What is the difference between summation notation and integral notation?

A: Summation notation is used to represent the sum of a discrete series of terms, while integral notation is employed to represent the continuous sum, or integral, of a function over a specific interval. 

Both notations involve a similar concept, but summation notation deals with discrete sequences, whereas integral notation is related to continuous functions.