To calculate result you have to disable your ad blocker first.
Cubic Equation Solver
To solve cubic equation input coefficients of a, b, c, & d and press calculate button using cubic equation solver
Cubic Equation Calculator
Find the roots of a third-degree polynomial with the help of a cubic equation calculator. This tool can find the three unknown real or imaginary roots of a polynomial equation of degree three.
It is the only cubic equation calculator available online that can provide the steps required for the roots’ calculation.
What is a cubic equation?
Like quadratic equations, it is also a polynomial equation. It has a maximum variable degree of three. This means it must have an x3.
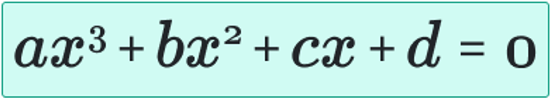
The general cubic equation looks like this:
“ax3 + bx2 + cx + d = 0”
where
- a, b, c, and d are coefficients and a ≠ 0.
Some examples of cubic polynomials are:
2x3 - 5x3 + 5x + 2-x3 - 1024x3 - x - 12x2 + 17
Notice that each expression has x3 as the leading term.
Roots of a cubic polynomial:
A linear equation has one root while a quadratic equation has two roots. Guess “How many roots does a cubic equation have?”. Three!
There can be two cases regarding these roots.
All three are real.One real, two complex.
A cubic polynomial always has one real root. In the second case, the complex roots are a pair of conjugates.
Cubic polynomial formula:
The formulas used to reduce cubic polynomials to their roots are pretty complex. Have a look:
- X1 = First root = S + T - b/3a
X2 = Second root = -(S + T)/2 + (S - T)* i√3/2 - b/3a
X3 = Third root = -(S + T)/2 - (S - T)* i√3/2 - b/3a
Here, b is the coefficient of x2.
To find the S and T, use the formulas written below.
S = ∛(R + √(Q³ + R²))
T=∛(R - √(Q³ + R²))
Letters a, b, c, and d are familiar. They are coefficients of the polynomial expression. But what are Q and R? If you fear that they are to be calculated then you are right!
Q = (3ac - b²) / (9a²)
R = (9abc - 27a²d - 2b³) / (54a³)
We feel sorry for you! But no worries, our cubic equation solver is here to save the day. Just punch in the coefficients and save yourself the trouble of going through this exhausting process of long calculations.
How do you solve a cubic equation?
Since the cubic formula is very long, several other ways in practice exist to solve the cubic polynomials. In this article, you will learn the formula method only.
- First thing first, arrange the equation in the standard form.
- After that write the coefficients separately.
- Find the Q and R values first.
- Then S and T.
- Now, use all these values to find the roots of the mentioned formulas.
Example:
Find the roots of the following cubic equation:
x3 + 2x2 + 3x + 12 = 0
Solution:
Step 1: Arrange in the standard form.
The equation is already in the standard form.
Step 2: Separate the coefficients.
a = 1
b = 2
c = 3
d = 12
Step 3: Find the Q and R values.
For Q
Q = (3ac - b²) / (9a²)
Q = (3(1)(3) - (2)²) / (9(1)²)
Q = 0.556
For R
R = (9abc - 27a²d - 2b³) / (54a³)
R = (9(1)(2)(3) - 27(1)2(12) - 2(2)3) / (54(1)3)
R = -5.2962
Step 4: Find S and T.
For S
S = ∛(R + √(Q³ + R²))
S = ∛(-5.2962) + √((0.556)³ + (-5.2962)²))
S = 0.2531
For T
T = ∛(R - √(Q³ + R²))
T = ∛(-5.2962) - √((0.556)³ + (-5.2962)²))
T = 2.1973
Step 5: Lastly, use the roots formula.
For First Root
X1 = S + T - b/3a
X1 = 0.2531 + 2.1973 - 2/3(1)
X1 = -2.6111
For Second Root
X2 = -(S + T)/2 + (S - T)* i√3/2 - b/3a
X2 = -(0.2531 + 2.1973)/2 + (0.2531 - 2.1973)* i√3/2 - 2/3(1)
X2 = -2.1218 + 2.12i
For Third Root
X3 = -(S + T)/2 - (S - T)* i√3/2 - b/3a
X3 = Third root = -(0.2531 + 2.1973)/2 - (0.2531 - 2.1973)* i√3/2 - 2/3(1)
X3 = -2.1218 - 2.12i

