To calculate result you have to disable your ad blocker first.

What is an Angle? Explained with Examples
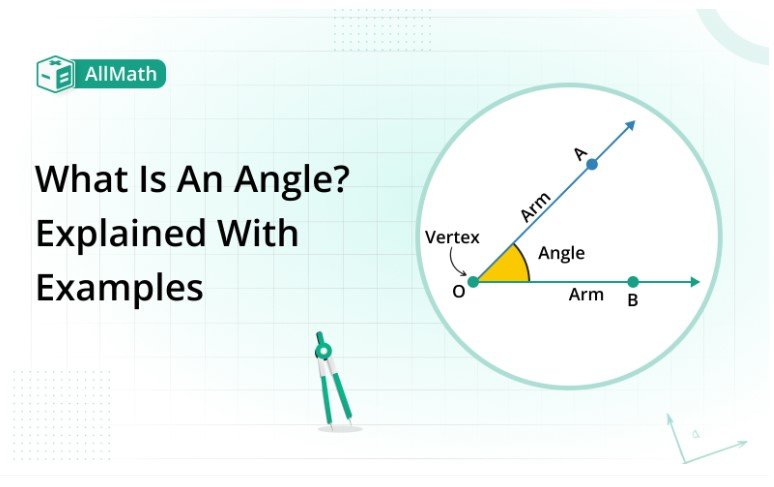
Table of Content
The ancient Egyptian and Mesopotamian civilizations introduced the concept of angles as an early system of measurement and geometry. They used angles to analyze the land, build up buildings, design roads, etc.
Then Greek scientists or mathematicians such as Thales, Pythagoras, and Euclid made a very important addition to the study of angles. Pythagoras’ theorem is known as the backbone of geometry and everyone is familiar with Euclidean geometry. These are the great contributions of Greek mathematicians.
What is an angle?
An angle is a shape / a figure formed by two rays when these rays contribute at a general endpoint known as the vertex of an angle. An angle is a measurement between different rays in the form of a radian or degree.
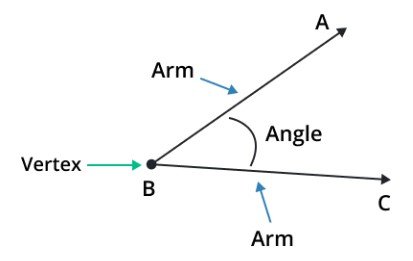
- Ray A is an upper-arm
- Ray C is a lower-arm
- The endpoint “B” where both rays meet is known as the vertex.
- The angle is a gap or a space between two lines that meet at a common point known as a vertex.
Types of Angles
Different types of angles are as follows:
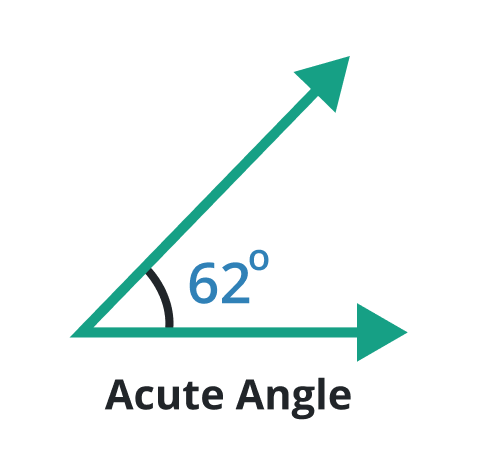
Acute angle
A type of angle in which the degree is always less than 90o is known as an acute angle. An acute angle is always sharp and narrow because the “space” which is known as the angle is very less between two rays.
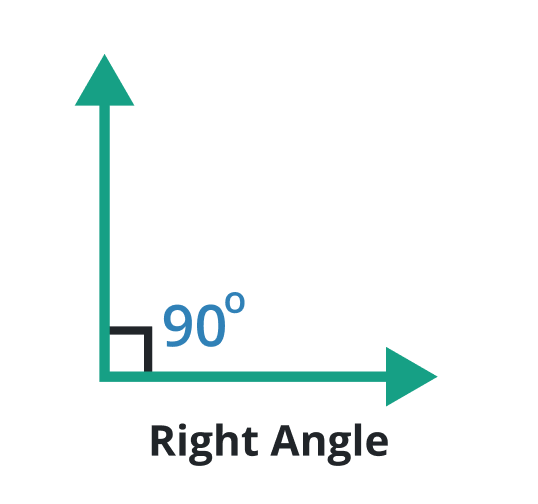
Right angle
A type of angle in which the degree is always equal to 90o is known as the right angle. At the right angle, the rays meet perpendicularly to each other at the endpoint.
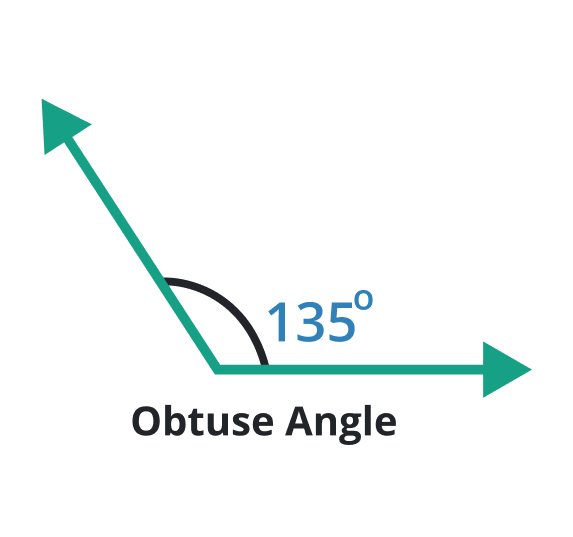
Obtuse angle
A type of angle having such a degree that lies between 90o and 180o is known as the obtuse angle. The obtuse angle is larger than the right angle. It is the wider angle.
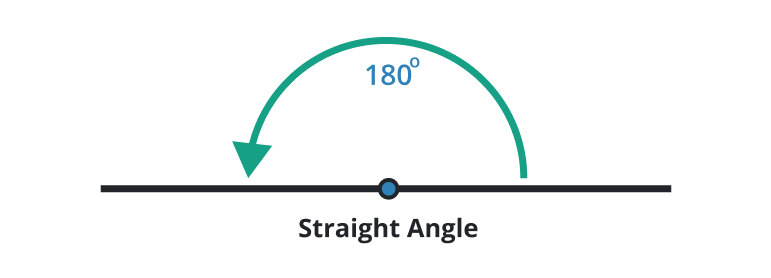
Straight angle
A type of angle in which the degree is 180o is known as the straight angle. The two rays oppositely meet each other at the vertex and form a straight line.
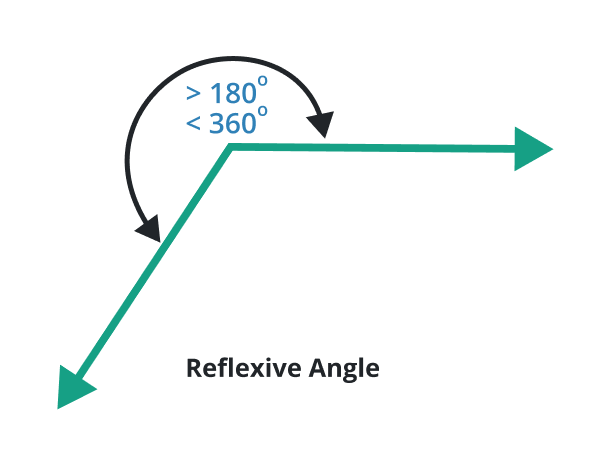
Reflexive angle
A type of angle which have a degree greater than 180o and less than 360o is known as the reflexive angle. This angle is formed when one of the sides of an angle rotates beyond a straight angle (180o) but doesn’t complete a full rotation.
Complete angle
A type of angle in which the degree is 360o is known as the complete angle. In this angle, a complete round trip is covered. It ends at a point from where it starts its rotation.

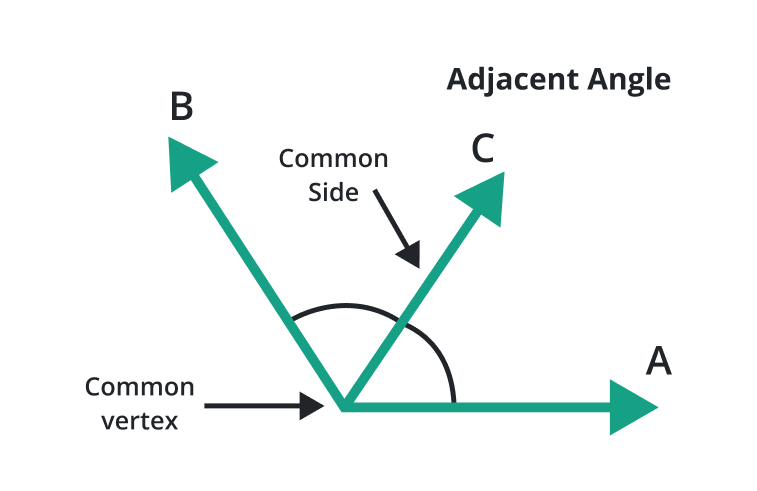
Adjacent angle
A pair of angles that share a common vertex or have the same endpoint is known as the adjacent angle. The common side made a line segment that connects the vertices of the adjacent angle.
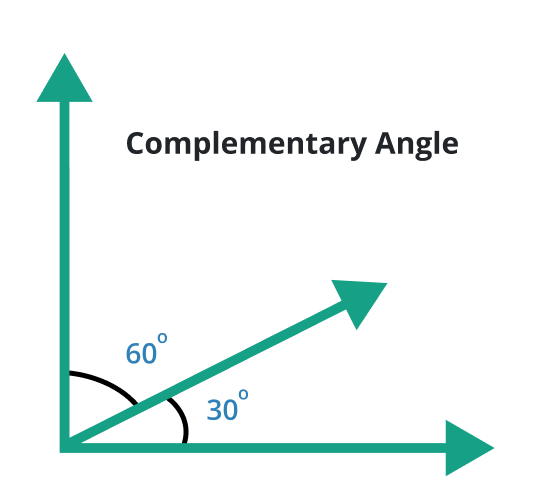
Complementary angle
A pair of angles whose sum is 90o is known as the complementary angle. In other words, we can say that the angle formed after the addition of two different angles and gives us the result of 90o is known as the complementary angle.
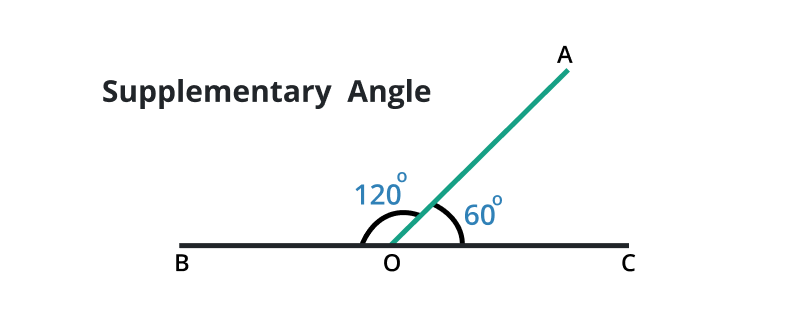
Supplementary angle
A pair of angles whose sum is 180o is known as the supplementary angle. Other than this, we can say that the angle formed after the addition of two different angles gives us the result of 180o is known as the supplementary angle.
Applications
Some applications of angle are as follows:
- Robotics and automation
- Computer graphics and animations
- Physics and mechanics
- Navigation and survey
- Engineering and Architecture
- Geometry and trigonometry
These are some applications of angles where angle plays a constructive role. Angle plays a very important role in all the above-mentioned fields.
Examples
Example 1:
In triangle ∆ABC, ∠A = 80o, and ∠B = 60o find ∠C =?
Solution:
Step 1: Add the ∠A, ∠B, and ∠C which is equal to 180o.
∠A + ∠B + ∠C = 180o
Step 2: Put the values of ∠A and ∠B.
80o + 60o + ∠C = 180o
Step 3: Simplification.
140o + ∠C = 180o
∠C = 180o - 140o
∠C = 40o
Example 2:
Determine the value of two angles A and B that are complementary, given that ∠A = (4x – 30) o & ∠B = (3x – 20) o.
Solution:
Step 1: By adding ∠A and ∠B it is equal to 90o as it is a complementary angle.
∠A + ∠B = 90o
Step 2: Substituting the values of ∠A and ∠B.
(4x – 30) o + (3x – 20) o = 90o
Step 3: Simplification.
(7x – 50) o = 90o
7x = 90o + 50o
7x = 140o
x = 140o / 7
x = 20o
Step 4: Put the value of “x” in ∠A.
∠A = (4x – 30) o
∠A = (4(20o) – 30) o
∠A = 80o – 30o
∠A = 50o
Step 5: Put the value of “x” in ∠B.
∠B = (3x – 20) o
∠B = (3(20o) – 20) o
∠B = 60o – 20o
∠B = 40o
Example 3:
Determine the value of two angles C and D that are supplementary, given that ∠C = (3y – 40) o & ∠D = (2y – 30) o.
Solution:
Step 1: By adding ∠C and ∠D it is equal to 180o as it is a supplementary angle.
∠C + ∠D = 180o
Step 2: By putting the values of ∠C and ∠D.
(3y – 40) o + (2y – 30) o = 180o
Step 3: Simplification.
(5y – 70) o = 180o
5y = 180o + 70o
5y = 250o
y = 250o / 5
y = 50o
Step 4: Put the value of “y” in ∠C.
∠C = (3y – 40) o
∠C = (3(50o) – 40) o
∠C = 150o – 40o
∠C = 110o
Step 5: Put the value of “y” in ∠D.
∠D = (2y – 30) o
∠D = (2(50o) – 30) o
∠D = 100o – 30o
∠D = 70o
Wrap up
In this article, we explain the angle in such a way that everyone can easily grab the basic concept of angle. An angle plays a very constructive role in the field of engineering, and in physics. Trigonometry is a major branch of mathematics and without these angles, it is considered nothing.
