To calculate result you have to disable your ad blocker first.

Diameter: Definition, Formula, and Examples

Table of Content
In the world of mathematics and beyond, the concept of diameter holds significant importance. Whether you're studying geometry, engineering, or even exploring the mysteries of the universe, understanding the diameter is essential.
In this article, we’ll cover the concept of diameter, its calculations, and applications in different fields
What is Diameter?
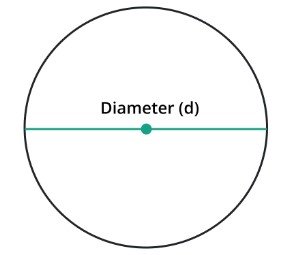
In mathematics, the diameter refers to the line segment that passes through the center of a circle or any other curved figure, connecting two points on its boundary. It is the longest chord in a circle.
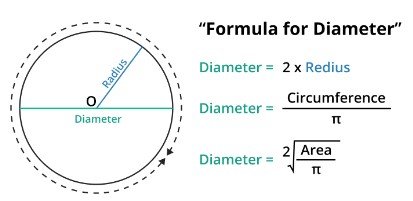
Formula of Diameter
By measuring the distance between any two locations on a circle's perimeter that are as far apart from the center as is practicable, we may find the diameter of the circle. The resulting value will be the diameter.
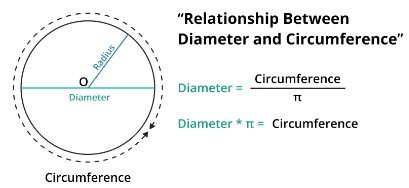
Relationship between Diameter and Circumference
The diameter and circumference of a circle are inseparably related. The circumference of a circle is the measurement of its outside edge, whereas the diameter is the length of the chord that passes through its center.
The circumference can be calculated using the diameter by employing the mathematical formula: Circumference = Diameter * π.
Exploring the Role of Diameter in Biology
The concept of diameter is not limited to the realm of mathematics and physical objects; it also finds relevance in biology. In biology, the diameter is used to measure the size of cells, blood vessels, or other microscopic structures. Understanding the diameter helps biologists comprehend the functionality and characteristics of living organisms.
Applications of Diameter in Real Life
Diameter in Geometry and Shapes
Many geometric forms, such as cylinders, ellipses, and circles, depend heavily on the diameter. It helps in establishing the various sizes, ratios, and connections between the components of the shapes.
Diameter in Engineering and Construction
Engineers and architects heavily rely on the concept of diameter while designing structures.
E.g.,
Knowing the diameter of the foundation pillars or boreholes is essential to maintaining structural integrity while building bridges or tunnels.
Astronomy and astrophysics
We must consider an object's diameter while evaluating it in the immensity of space. Astronomers use the diameter to determine the sizes of galaxies, planets, stars, and even the universe itself.
Examples
Example 1:
Find the diameter of the circular air base when the circumference of that base is 40 units.
Solution:
Step 1: Firstly, write the given data.
C = 40 units
Pi = 3.14
D =?
Step 2: Write the formula of diameter.
D = C / pi
Step 3: Substitute the values in above mentioned formula.
D = 40 / 3.14
D = 12.74 units
So, the diameter of the circular base is 12.74 units.
Example 2
The diameter of a circular track is 10 units. What would be the circumference of the track?
Solution:
Step 1: Write the given data.
D = 10 units
Pi = 3.14
C =?
Step 2: Write the formula of circumference.
C = pi * D
Step 3: Substitute the values in above mentioned formula.
C = 3.14 * 10
C = 31.4 units
So, the circumference of the circular track is 31.4 units.
Example 3
Find the radius of a circular ring if the diameter of the ring is 5 units.
Solution:
Step 1: Write the given data.
D = 5 units
R =?
Step 2: Write the formula of radius.
R = D / 2
Step 3: Substitute the values in above mentioned formula.
R = 5 / 2
R = 2.5 units
So, the Radius of the circular ring is 2.5 units.
Conclusion
The diameter is a fundamental concept in various fields. Its significance is seen in many academic disciplines and enables us to understand the length, breadth, or area of various str
