To calculate result you have to disable your ad blocker first.

Indirect Measurement: Definition, Methods, and Examples

Table of Content
Indirect measurement is a mathematical technique that uses proportions to determine unidentified lengths or distances in the same figures. This technique is used when direct measurement is impossible due to physical limitations, safety concerns, or inaccessibility.
In indirect measurement, you compare the measurements of corresponding sides of two similar figures and then use the concept of proportions to find the unknown measurement. We will explore the concept of the indirect method in this article along with the definition, applications, and calculations.
What is Indirect Measurement?
The indirect method of measurement involves using proportions to calculate unknown lengths or distances within the same figures. It is used when we cannot measure something directly. We can use this method to measure the width of a river or the height of an object by using its shadow or other available data.
The process involves creating triangle models based on the given scenario. We then use similar triangles and proportional to calculate the desired value. It is a reliable approach to providing accurate results even when direct measurement is challenging.
Explanation
Imagine a person standing in front of a tree while the sun is shining, and we assume the sun's angle remains constant. The shadows cast by both the person and the tree form two similar triangles. The angles of these triangles are equivalent and their sides are in proportion.
We can apply the principles of indirect measurement by drawing a line from the top of the tree and the person to the end of their respective shadows. We then compare the lengths of the corresponding sides of the two triangles, which allows us to establish proportions and calculate the height of the tree indirectly. This technique is clever and effective when direct measurement tools are unavailable.
Methods for Indirect Measurement
We are going to learn three different methods for indirect Methods.
- similar triangles
- Proportionality
- Pythagorean Theorem
Indirect Measurement by using a Similar Triangle
This method involves setting up similar triangles. Similar triangles that have similar shapes but possibly different sizes. If you can find two similar triangles that have a known side in common, then you can use the ratio of the other sides to find the unknown side.
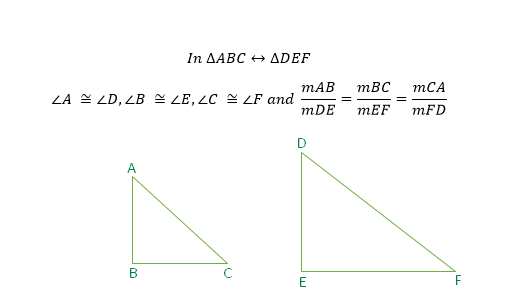
Indirect Measurement by using proportionality
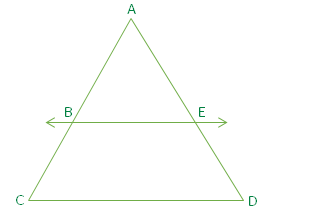
Proportionality Theorem states, “If a line is drawn parallel to one side of a triangle, it divides the other two sides proportionally”. This theorem can be used to discover unknown measurements of similar triangles by comparing the ratios of the sides. Problems involving indirect measurement can be effectively solved by using these principles.
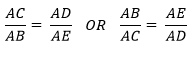
Indirect Measurement by using the Pythagorean Theorem
The Pythagorean Theorem is a fundamental mathematical principle used to make a relationship between the three sides of a right-angle triangle. It states “In any right-angle triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides”.
c2 = b2 + a2
Tips for using proportions in indirect measurement
- Ensure that the two figures you are comparing are similar. They are similar in shape but may have different sizes.
- Be certain that your measurements are precise. The accuracy of your measurements will affect the accuracy of your results.
- Be careful of units. Ensure that all of your measurements are expressed in the same unit.
Examples of Indirect Measurement
Example 1:
Find the length of the unknown side in a right-angle triangle using the Pythagorean Theorem.
If side a = 4 cm and c = 9 cm.
Solution:
Given, a = 4cm, c = 9cm, and b =?
As we know that
c2 = b2 + a2
Put the given values in the Pythagorean formula
(9cm) 2 = b2 + (4cm)2
81cm2 = b2 + 16cm2
81 cm2 - 16 cm2= b2
65 cm2 = b2
After taking square root on both sides, we get
b = 8.06cm
Example 2:
In the triangle, ACD shown in the figure, CD parallel to BE
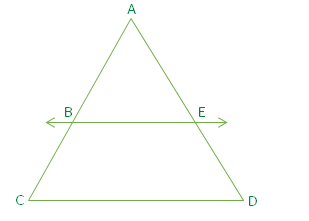
If AB = 5cm, AC = 6cm, and AD = 4.4 cm then find AE.
Solution
By using the Proportionality theorem
![]()
Put the given value in the above equation
5/6 = AE/4.4
0.833 × 4.4 = AE
3.6652 = AE
Thus, AE = 3.6652 cm
Conclusion
In this article, we have discussed the definition of indirect measurement. We've learned different methods of indirect measurement to determine the unknown length. We solved some examples for our readers to understand it better.
