To calculate result you have to disable your ad blocker first.

Intersecting Lines: Definition, Types, Properties, and Examples
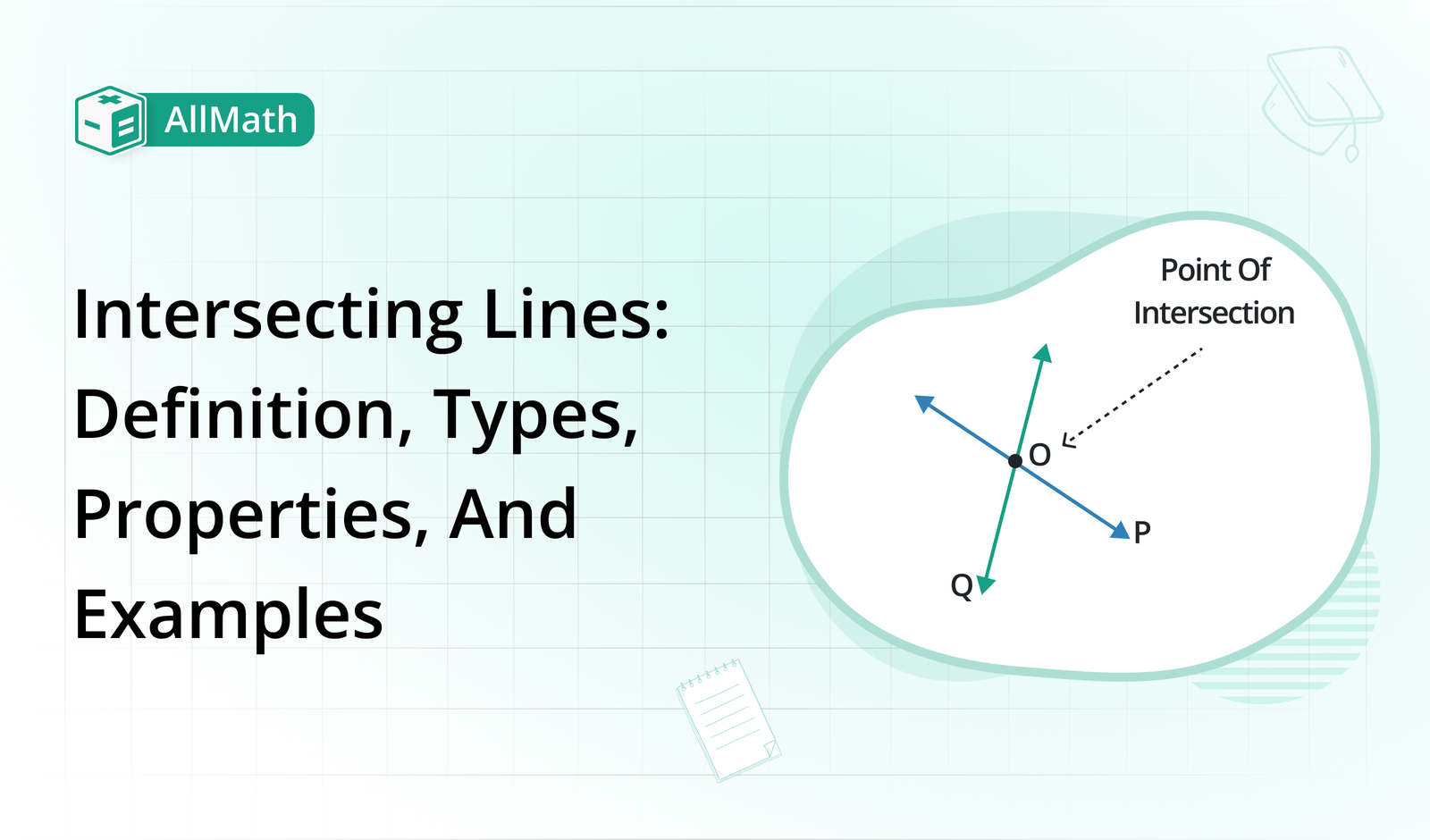
Table of Content
Before exploring intersecting lines, it is essential to define a line. Lines are one-dimensional shapes that stretch in both directions infinitely. Lines with two ends are referred to as line segments. A line intersecting at a common point is called an intersecting line in Geometry.
The intersection of these lines creates a fascinating dynamic with various implications and applications. We will explore their properties, delve into the mathematical theories, and discover their significance across different fields.
Intersecting Lines
Two or more Lines that intersect or meet at a single point are referred to as intersecting lines. Points of intersection are the points where these lines intersect. The following figure shows two intersecting lines, P and Q, and the point of intersection is labeled O.

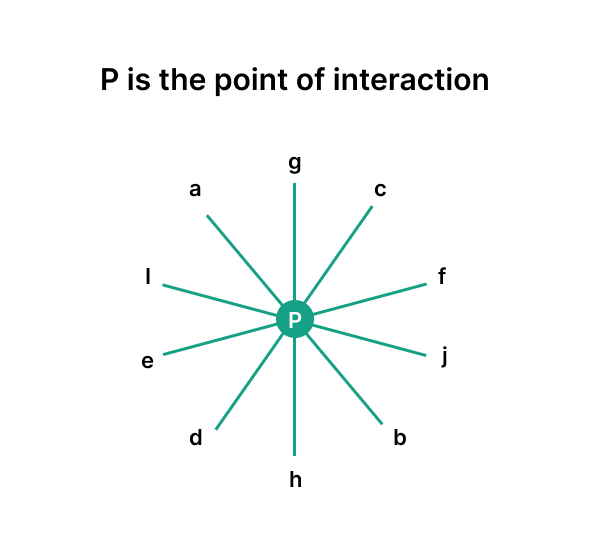
Several straight lines cross and meet at the common point P in another example.
Formula to Calculate Interaction Point
There are different methods available to find the intersection point of two lines represented in the form of linear equations. Here we will use Cramer’s rule for this purpose.
Suppose P and Q are straight lines that intersect at point O.
To find the coordinates (x1, y1) of the intersection point of lines P and Q, given their equations:
P: a1x1 + b1y1 + c1 = 0
Q: a2x + b2y2 + c2 = 0
The formula we have derived using the Cramer rule is used to calculate the coordinates of the intersection point as:
(x1, y1) = [(b1c2 - b2c1) / (a1b2 - a2b1), (c1a2 - c2a1) / (a1b2 - a2b1)]
This formula allows you to find the exact point where the two lines intersect in a two-dimensional Cartesian coordinate system.
Types of Intersecting Lines
There are several types of intersecting lines based on the angles they form and their relationships with each other. Some common types of intersecting lines are given below:
Perpendicular Lines: Two lines that intersect at a 90°angle are referred to as perpendicular lines.
Oblique Lines: These are intersecting lines that are neither perpendicular nor parallel to each other. They intersect at various angles other than 90 degrees.
Angular Bisector Lines: A line that intersects an angle and divides it into two equal angles is called an angular bisector line.
Concurrent Lines: Concurrent lines are three or more lines that cross at a single point. The point of concurrency is the point at which they cross.
Key Properties of Intersecting Lines
The following characteristics of intersecting lines help us recognize them:
- There is only one point where intersecting lines meet.
- Intersecting lines can meet at any angle that is greater than 0° but less than 180°.
- Two Straight Lines Never Share Multiple Intersection Points. If they do, they will not be called intersecting lines.
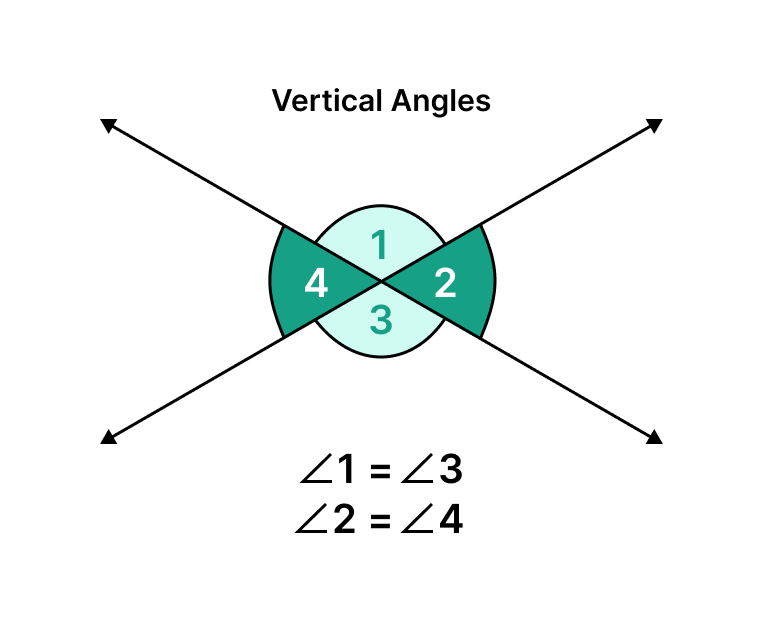
- When two lines intersect, they create a set of angles known as vertical angles. These angles share a vertex at the point of intersection and point in opposite directions, facing each other. It is important to note that the vertical angles formed by intersecting lines are always equal in measure.
In the following figure, ∠1 and ∠3 represent vertical angles, and they share the property of being equal to each other. ∠2 and ∠4 are also vertical angles, and they display equality.
Examples of Intersecting Lines in the Real-World
- Road Intersections: One of the most common real-world examples of intersecting lines is road intersections. At a junction, two or more roadways come together to create intersecting lines. Traffic lights and signs are strategically placed to control the flow of vehicles and ensure safety at these intersections.
- Scissors: Another familiar example of intersecting lines can be found in scissors. The two arms of the scissors form intersecting lines.
- Crosswalks: Crosswalks, which are marked by intersecting lines on roads, help pedestrians cross safely.
Numerical Examples of Intersecting Line
Example 1:
Find out the point of intersection of line 9x + 5y + 7 = 0 and 5x + 3y + 1 = 0 using the point of intersection formula.
Solution:
Line 1: 9x + 5y + 7 = 0
Line 2: 5x + 3y + 1 = 0
Suppose point of intersection = (x1, y1)
Here,
a1 = 9, b1 = 5, c1 = 7
a2 = 5, b2 = 3, c2 = 1
∴ (x1, y1) = [(b1c2 - b2c1) / (a1b2 - a2b1), (c1a2 - c2a1) / (a1b2 - a2b1)]
Substitute the given values in the point of intersection formula
(x1, y1) = [(5.1 – 3.7) / (9.3 – 5.5), (7.5 – 1.9) / (9.3 – 5.5)]
= [(5 – 21) / (27 – 25), (35 – 9) / (27 – 25)]
= (– 16/2, 26/2)
= (– 8, 13)
Hence, (−8, 13) is the point of intersection of 9x + 5y + 7 = 0 and 5x + 3y + 1 = 0.
Example 2:
Find the point of intersection of the lines 2x + 3y – 5 = 0 and 4x – 2y + 6 = 0 using the point of intersection formula.
Solution:
Line 1: 2x + 3y – 5 = 0
Line 2: 4x – 2y + 6 = 0
Let's denote the point of intersection as (x1, y1).
a1 = 2, b1 = 3, c1 = – 5
a2 = 4, b2 = – 2, c2 = 6
Put these values in the point of intersection formula.
∴ (x1, y1) = [(b1c2 - b2c1) / (a1b2 - a2b1), (c1a2 - c2a1) / (a1b2 - a2b1)]
(x1, y1) = [((3) (6) – (– 2) (– 5)) / ((2) (– 2) – (4) (3)), ((– 5) (4) – (6) (2)) / ((2) (– 2) – (4) (3))]
= [(18 – 10) / (– 4 – 12), (– 20 – 12) / (– 4 – 12)]
= [(8 / – 16), (– 32 / – 16)]
= (–1/2, 2)
Thus, the point of intersection of the lines 2x + 3y – 5 = 0 and 4x – 2y + 6 = 0 is (–1/2, 2).
Conclusion:
In this article, we have covered intersecting lines, their types, and applications. We have explained the intersection point formula and highlighted key properties. We have used real-world examples to provide practical context, and a numerical example has illustrated the use of the formula.
