To calculate result you have to disable your ad blocker first.

Surface Area: Definition, Formulas, Applications, and Examples
Publish Date: 08 Aug, 2023
Table of Content
Mathematics is an interesting subject that covers a wide range of branches and ideas. One essential concept in mathematics is area. By understanding the concept of area, we can measure and quantify the size of two-dimensional shapes.
It provides us with valuable information about their properties and how they relate to one another. The area helps us gain insights into the characteristics and interactions of these shapes. We shall examine the idea of the area, its uses, and its importance in both mathematics and daily life in this article.
What is an Area?
The area is the measurement of the surface that a two-dimensional form encloses. It gives us knowledge of the volume occupied by a shape, such as a circle, square, rectangle, or triangle. The area may be stated in square units like square centimeters “cm2” or square meters “m2”, depending on the circumstance.
The calculation of area depends on the type of shape under observation. The area of regular forms like squares and rectangles may be calculated by multiplying the length and width of a shape. When a triangle is involved, the area may be determined by multiplying the base length by the triangle's height, divided by two. The radius “r” square multiplied by “π” will provide the area of a circle.
Formulas for the Area of different shapes
Here are a few geometrical shapes and their formulas for finding the surface area
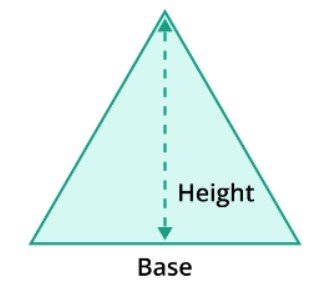
Area of Triangle
The area of the triangle is as follows:
Area =1 / 2 *(height)*(base)
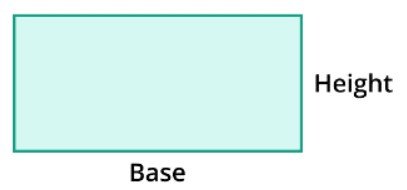
Area of Rectangle
The area of a rectangle is as follows:
Area = base * height
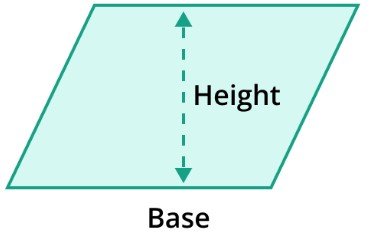
Area of Parallelogram
The area of a parallelogram is as follows:
Area = base * height
Area of Rhombus
The area of a rhombus is as follows:
Area = 1 / 2 * diagonal * diagonal
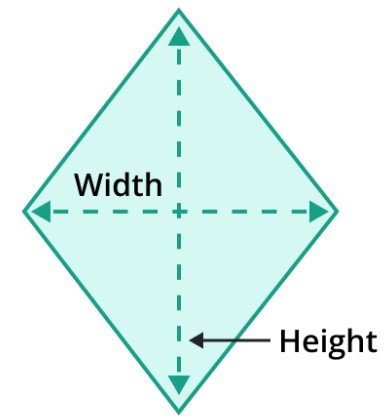
Area of Trapezium
The area of a trapezium is as follows:
Area = 1 / 2*(a + b) *h
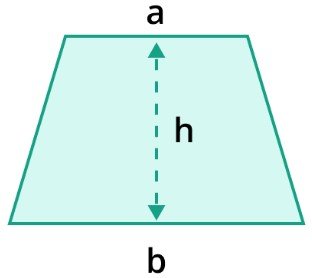
Area of Circle
The area of a circle is as follows:
Area = π*r2
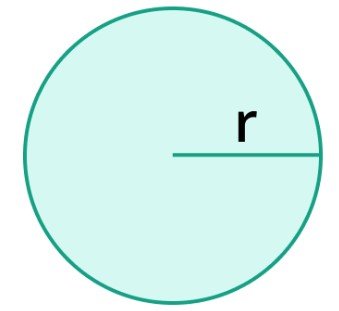
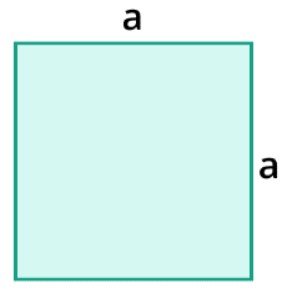
Area of Square
The area of the square is as follows:
Area = a*a
Advanced Concepts in Area
Beyond basic shapes, the concept of the area extends to more complex figures. Some advanced concepts related to the area include:
Composite Figures
Composite figures are formed by combining multiple basic shapes. To calculate the area of a composite figure, it is divided into simpler shapes, and their individual areas are calculated. The overall area of the composite figure is then calculated by adding these areas together.
Integration and Calculus
In calculus, integration is used to find the area under curves. This technique allows us to determine the area of irregular shapes and solve complex mathematical problems related to the area.
Three-Dimensional Figures
The area is generally concerned with two-dimensional forms, although it also has uses in three-dimensional objects. The idea of area and the surface area of three-dimensional objects like cubes, cylinders, and spheres are intimately connected.
Applications of Area in Real Life
The area has many practical applications in our daily lives, ranging from construction and architecture to farming and art.
Architectural Design
Architects and engineers depend on area calculations to determine the space requirements for building designs. By understanding the area, they can plan for rooms, corridors, and other architectural elements properly.
Landscaping and Gardening
In landscaping, knowing the area helps determine the amount of soil, grass, or plants needed to cover a particular space. It helps to optimize resources and achieve balanced and pleasing outdoor spaces.
Painting and Flooring
When painting a room or installing new flooring, knowing the area allows for accurate estimations of the required amount of paint or flooring materials. This helps in budgeting and reducing wastage.
Agriculture and Farming
Farmers use area calculations to determine the size of their fields, enabling them to plan irrigation, fertilization, and crop rotation effectively. It ensures optimal usage of resources and maximizes crop yield.
Geometry and Design
The area plays an important role in geometric and design-related fields. Architects, graphic designers, and artists use the concept of area to create visually engaging compositions, ensuring a mixed balance of shapes and forms.
Examples
Some examples of finding different types of areas are as follows:
Example 1
A big rope is in a round shape. It has a 100-unit radius. Find its Area?
Solution:
Step 1: Write a given data.
r = 100 units
π = 3.14
Step 2: As the rope is in a circular shape. So, we use a circular formula.
Area = π*r2
Step 3: Substitute the values in a given formula.
Area = (3.14) *(100)2
Area = (3.14) *(10000)
Area = 31400 units2
Example 2:
If a rectangle's base and height are 10 cm and 2 cm, respectively, determine its area.
Solution:
Step 1: Write a given data.
base = 10 cm
height = 2 cm
Step 2: Write the formula of a rectangle.
Area = base * height
Step 3: Substitute the values in a given formula.
Area = (10) * (2)
Area = 20 cm2
Example 3:
Find the area of a rectangle if it has a base is 40 m and a height is 0.5 m.
Solution:
Step 1: Write a given data.
base = 40 m
height = 0.5 m
Step 2: Write the formula of a rectangle.
Area =1 / 2 *(height)*(base)
Step 3: Substitute the values in a given formula.
Area =1 / 2 *(0.5) *(40)
Area = 10 m2
Conclusion
The concept of area is fundamental to mathematics and has several uses across many academic fields. It enables us to solve real-world issues and ability to good conclusions helping us comprehend the dimensions, connections, and interactions of two-dimensional forms.
