To calculate result you have to disable your ad blocker first.

Null Set: Definition, Properties, Applications, and Examples
Table of Content
Sets play an important role in defining relationships and categorizing elements in the study of mathematics, especially in set theory. Among these sets the concept of the null set which is also known as the empty set holds significant importance. Understanding the characteristics and applications of the null set can provide valuable insights into different mathematical domains and real-life scenarios.
The Null Set is beneficial despite its empty nature. It plays a key role in defining relationships and set operations as well as probability theory as a set without any elements. While seemingly simple the applications of null sets expand to mathematical discipline making it an important concept to study mathematics.
In this article, we will cover the concept of a null set along with its definition, properties, and applications. we will also provide useful examples to pick up this concept exactly.
Definition of a Null Set
A null set is a unique set, which contains no elements. In other words, it can be defined as a set without any objects or elements. The null set is denoted as ∅ and is pronounced as an empty set or { } which symbolizes its empty nature. The null set may seem simple but its significance lies in the foundations of set theory and different mathematical rules.
- It has zero elements making it distinctive from all other kinds of sets.
- The Null Set is considered a valid and essential concept in mathematics and set theory.
Properties of a Null Set:
The Null Set has useful and important properties that distinguish it from other sets:
Cardinality of a Null Set
The cardinality of a set is the number of elements present in the set. For the Null Set, its cardinality is always zero. The concept of cardinality establishes the significance of the null set in core dimensions of mathematics especially in the discipline of the set theory.

Union with Other Sets
The union of sets signifies the combination of all elements from the sets under study. When we apply the operation of the union of the null set with any other set the result will be the set itself. This is because the null set contributes no elements and the other set remains unchanged.
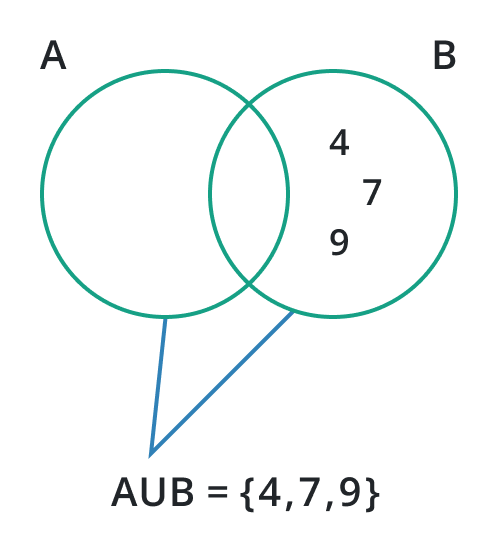
Intersection with Other Sets
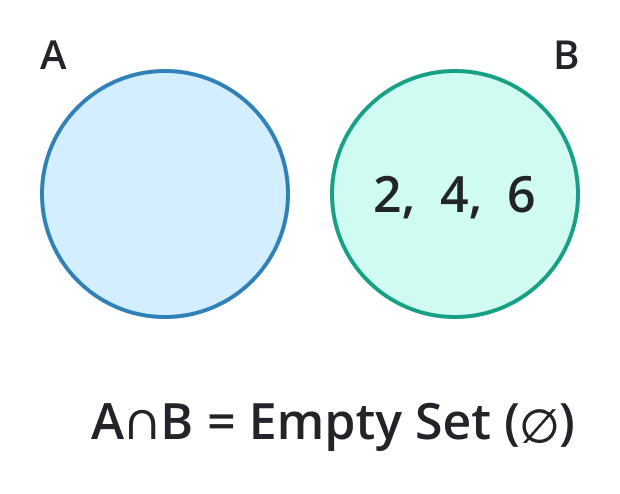
The intersection (which is denoted by ∩) of the null set with any set A results in the null set (∅) itself. This property is called the identity property of the intersection.
For example, if we have a set A (empty set) and B = {2, 4, 6}, the intersection of B with the null set (∅) will be the null set.
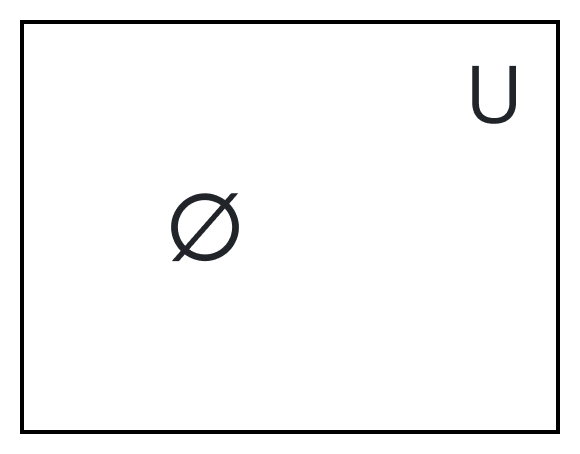
Complement of a Null Set
The complement of the null set (∅) with respect to any universal set U will be the entire or whole universal set U itself. This is because the null set contains no elements. So its complement includes all elements in the universal set. Thus, the complement of (∅) is U.
Importance of Null Sets in Various Fields
Set Theory: The null set is important in defining subsets and set operations. It serves as the base case for various set relationships.
Precision in Mathematics: In mathematical proofs and reasoning, the null set helps to establish precise definitions and boundaries which enables mathematicians to tackle special cases and empty solutions effectively.
Handling Data in Computer Science: In computer programming and data analysis, the null set plays a crucial role in managing missing or undefined values. It ensures the accurate computations and data handling.
Linear Algebra: The null space of a matrix refers to the set of all solutions to the homogeneous equation Ax = 0 in the study of linear algebra. It is the essence of the solution set of a null set.
Real-Life Implications of Null Set
The null set in real-world scenarios plays a key role. Some of the applications of the null set in everyday life are discussed below:
Online Shopping Carts
When a user has no items in their shopping cart, it can be represented as a null set which denotes the absence of products.
Weather Forecasting
The concept of a null set is employed to predict the probability of extreme weather events in weather forecasting that can have no chance of occurrence.
Venn Diagrams
Venn diagrams frequently include the null set to represent no elements belonging to certain sets.
Mathematics
The null set finds application in different areas such as probability theory, combinatorics, and algebra in the field of mathematics. It plays a crucial role in defining empty solutions to equations and understanding the concept of an empty event in probability.
Computer Science
In computer science, the null set is of great significance. It is often used to represent the absence of data or a missing value in databases, programming languages, and algorithms.
Examples of Null Sets:
To comprehend the concept better, let's explore some examples of null sets.
Example 1:
Suppose we have the following sets:
- Set X = {x ∈ N | x > 10}
- Set Y = {y ∈ R | y < 0}
- Set Z = {z ∈ Z | z is odd}
Now, let us identify the null sets from these examples:
- Set X' = {x ∈ N | x > 100} - Here, X' is a null set as no natural number is greater than 100.
- Set Y' = {y ∈ R | y > 100} - Y' is a null set since no real number is less than 0.
- Set Z' = {z ∈ Z | z is even} - Z' is a null set as there are no odd integers in the given set Z.
Example 2:
Consider
Set M = {x ∈ P | x is prime}
Now let’s identify the null set from this set.
Set M' = {x ∈ M | x is composite}
Now if we compute the intersection of M & M', it would be a null set as prime numbers have no common elements with composite numbers.
