To calculate result you have to disable your ad blocker first.
Synthetic Division Calculator
To use a synthetic division calculator, enter a polynomial & a linear factor and hit calculate button
Table of Contents:
Synthetic Division Calculator
Synthetic division calculator is a tool that performs synthetic division by using the polynomial as a numerator and linear factor as a denominator. The synthetic division calculator gives a step-by-step solution to every problem.
Definition of Synthetic division
Synthetic division is a method of dividing polynomials by linear factors. It is a very simple technique to divide the polynomial with the linear factor of the form “x-c”. Where “c” is a self-determined constant.
Formula
The formula of synthetic division is stated as follows.
P(x)/(x-c) = Q(x) + R/(x-c)
Where,
- P(x) = dividend polynomial of any order.
- (x-c) = linear factor of degree 1.
- Q(x) = quotient polynomial formed after applying the synthetic technique.
- R = constant quantity is known as the residual or remainder.
Example of Synthetic Division
Solve the question by synthetic division if,
Numerator polynomial = 7x4+2x2-2
Denominator polynomial = x-2
Solution:
Step 1: Write the given data.
P(x) = 7x4+2x2-2
Linear factor = x-2
P(x)/Linear factor = (7x4+2x2-2)/ (x-2)
Step 2: Write the coefficients of the numerator polynomial and write them from greatest to least.
7, 0, 2, 0, −2
Step 3: Put the denominator term equal to zero and find the value of the unknown variable.
x−2=0
x=2
Step 4: Write the above data in the synthetic division and simplify.
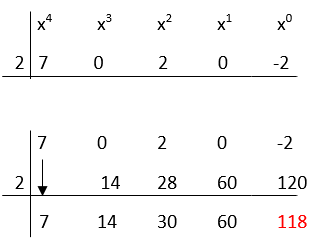
The quotient is 7x3 + 14x2 + 30x + 60 and the remainder is 118.
Step 5: Write the value according to the synthetic division formula.
Q(x) = 7x3 + 14x2 + 30x + 60, R = 118, and c = 2
[7x4+2x2-2/ x-2] = (7x3 + 14x2 + 30x + 60) + [118/ (x-2)]
Some other examples
Here are a few results of other examples in the table section.
Numerator Polynomial | Denominator Polynomial | Quotient | Remainder |
7x5+2x2-2 | x - 5 | 7x4+35x3+175x2+877x+4385 | 21923 |
7x3+4x2+3 | x - 4 | 7x2+32x+128 | 515 |
x3+7x2+3 | x-2 | x2+9x+18 | 39 |
x5+7x2+3 | x-4 | x4+4x3+16x2+71x+284 | 1139 |
x6-x3+3 | x-2 | x5+2x4+4x3+7x2+14x+28 | 59 |

