To calculate result you have to disable your ad blocker first.

Addition: Definition, Properties, and Examples
Publish Date: 08 Aug, 2023
Table of Content
The concept of addition is fundamental to mathematics and has a long history that dates back thousands of years. The exact origins of addition are difficult to trace. However, mathematicians during the period from the 16th to the 19th centuries, such as François Viète, John Napier, and Gottfried Wilhelm Leibniz, made significant advancements in algebra and the development of mathematical notation.
They refined and standardized methods of addition and introduced symbols and notation that we still use today. In this article, we will discuss the concept of addition, its properties, and solve some examples for better understanding.
What is Addition?
Addition is an arithmetic operation where two or more numbers are combined to give a larger number, known as the sum or addition.
We can also say that when given two numbers, called addends, the sum or result of addition is obtained by combining the addends. The addends are added together using the addition operation, resulting in a single value known as the sum.
For example:
In the expression “3 + 5”, the number “3” and the number “5” are the addends, and the sum is “8”.
Addition with Multiple Addends
When adding multiple addends, whether they are numbers or expressions, you can follow these steps to ensure an accurate sum:
- Start by writing down all the addends in a horizontal line, aligning them vertically so that the one digit of each addend is in the same column.
- Begin by adding the digits in the rightmost column (one’s column) together.
- If the sum of the digits in a column is 10 or greater, carry over the value of 1 to the next column on the left. Write down the rightmost digit of the sum in the current column.
- Move to the next column on the left and add the digits in that column, along with any carried-over value from the previous step. Again, if the sum is 10 or greater, carry over the value of 1 to the next column.
- Repeat this process for each column, moving from right to left, until all the columns have been added.
- Once you have added all the columns, the resulting sum will be the final answer.
Here are some examples of addition with multiple addends:
9 + 4 + 7 = 2015 + 6 + 1 = 22
Addition with Decimals and Fractions
When adding decimals and fractions, there are specific methods to follow. Here is an explanation of how to add decimals and fractions separately.
To add decimals
- The decimal points of the numbers are added after alignment.
- Starting from the rightmost column add the digits in each column.
- If there is a carry-over when adding the digits in a column, carry it over to the next column.
- Write the sum with the decimal point in the same position as the original numbers.
Here are some examples of Addition with Decimals:
35 + 1.27 = 3.6225 + 4.75 = 6.0
To Add Fractions
- Find a common denominator by finding the denominators' least common multiple (LCM).
- Each fraction should be rewritten using the same denominator.
- Add the numerators of the fractions.
- Keep the denominator the same.
- Simplify the fraction, if possible, by reducing it to its simplest form.
Here are some examples of Addition with Fractions:
1/4 + 3/8 = 5/821/12 + 32/12 = 53/12
Addition with Algebraic expression:
The procedure for adding algebraic expressions involves the following steps:
- Search for words where the same variables have been raised to the same powers.
- The coefficients of related terms can be added or subtracted.
- Rewrite the expression by combining the like terms and maintaining the order of the terms.
For example:
3x + 2y - 5x + 4y = -2x + 6y5x -y + 2x -3y = 7x – 4y
Properties of Addition
The following are the properties involving addition:
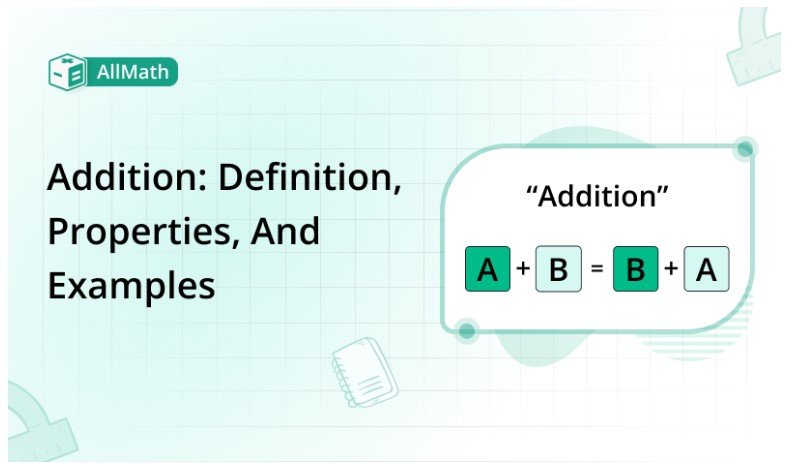
Commutative property:
The order in which the numbers are added has no bearing on the result, according to the commutative property.
Associative property:
According to the associative property, the order in which the numbers are added has no bearing on the outcome.
Identity property:
The identity property states that adding zero to a number leaves the number unchanged.
Inverse property:
The inverse property states that for every number, there exists an additive inverse such that adding the number and its additive inverse gives zero.
Closure property:
The closure property states that the sum of any two numbers in a given set of numbers will always belong to that same set.
Examples of Addition
Example 1:
Add (2x2 + 3x + 4) and (-x2 + 5x – 2)
Solution:
Take given terms, write like terms together, and simplify them.
(2x2 + 3x + 4) + (-x2 + 5x – 2)
= 2x2 – x2 + 3x + 5x + 4 – 2
= x2 + 8x + 2
Example 2:
Add (2 + 3 + 4) and (2 + 5 – 2)
Solution:
Take the given terms and solve the brackets first
(2 + 3 + 4) + (2 + 5 – 2)
= (9) + (5)
= 14
Hence.
(2 + 3 + 4) + (2 + 5 – 2) = 14
