To calculate result you have to disable your ad blocker first.

Inequality in Mathematics: Definition, Types, and Examples

Table of Content
An inequality is a mathematical statement that expresses a relationship of comparison between two expressions. It describes how one quantity is related to another in terms of being greater than, less than, greater than, or equal to, or less than or equal to. In this article, we will explore inequalities' definitions, types, and properties. We will learn how to solve inequalities through illustrative examples.
Definition of Inequality
Inequality is a way of comparing two numbers or expressions to see which value is greater, smaller, or possibly equal to the other. We use special symbols like > (greater than), < (less than), ≥ (greater than or equal to), or ≤ (less than or equal to) to represent these comparisons. These symbols are referred to as inequality signs. The inequalities > and < are known as strict (or strong) whereas the inequalities ≤ and ≥ are called non-strict (or weak).
Understanding the Notation of Inequalities
Now let's examine the notation used to indicate inequalities. These symbols are essential to convey the relationship between the quantities involved.
- < (Less Than): This symbol denotes that the value on the left is smaller than the value on the right. For instance, 2 < 5 means two is less than five.
- > (Greater Than): This symbol signifies that the value on the left is larger than the value on the right. For example, 7 > 4 means seven is greater than four.
- ≤ (Less Than or Equal To): This symbol indicates that the value on the left is either smaller than or equal to the value on the right. For instance, 3 ≤ 3 means three is less than or equal to three.
- ≥ (Greater Than or Equal To): This symbol expresses that the value on the left is either larger than or equal to the value on the right. For example, 9 ≥ 6 means nine is greater than or equal to six.
Types of Inequalities
Inequality in mathematics can be divided into several types based on the mathematical operations involved. The most common types of inequalities are given below.
- Linear Inequalities
Linear inequalities involve expressions with variables raised to the power of one. The general form of a linear inequality is ax + b < c or ax + b > c, where a, b, and c are constants, and x is the variable.
Example:
- 3x + 5 > 10
- 2x - 4 < 6
Linear inequalities play a crucial role in graphing straight lines and defining regions on a coordinate plane.
- Rational Inequalities
Expressions with fractions having polynomial terms in the numerator and denominator are included in rational inequalities. Solving rational inequalities requires considering the critical points where the denominator becomes zero.
Example:
- (x - 3) / (x + 2) > 0
- (2x2 - 5x) / (x - 1) ≤ 0
Rational inequalities are common in real-world applications, especially when rates or proportions are involved.
- Absolute Value Inequalities
Absolute value inequalities involve expressions containing the absolute value of a variable. The general form of an absolute value inequality is |ax + b| < c or |ax + b| > c, where a, b, and c are constants.
Example:
- |2x - 4| < 8
- |3x + 5| > 10
Absolute value inequalities occur in distance measurements and modulus functions.
Properties of Inequalities
Understanding the properties of inequalities is essential for solving complex mathematical problems. Let's look into some important properties.
Law of Trichotomy
For any a, b ∈ R, one and only one of the following statements is true.
a < b or a = b, or a > b
A special case of this property is the case for b = 0; namely,
a < 0 or a = 0, or a > 0 or any a ∈R
Addition Property
- If a > b, then a + c > b + c
- If a < b, then a + c < b + c
Subtraction Property
The subtraction property of inequalities states, “If you subtract the same value from both sides of an inequality, the inequality remains true”.
- If a < b, then a - c < b – c
- If a > b, then a - c > b – c
Multiplication Property
The multiplication property of inequalities states “If you multiply both sides of an inequality by the same positive value, the inequality remains true. However, the inequality sign must be reversed if you multiply by a negative value”.
- If a > b and c > 0, then ac > bc
- If a > b and c < 0, then ac < bc
Division Property
The division property of inequalities states, “If you divide both sides of an inequality by the same positive value, the inequality remains true. However if you divide by a negative value, the inequality sign must be reversed”.
- If a < b and c > 0, then a/c < b/c
- If a < b and c < 0, then a/c > b/c
Transitive Property
The transitive property of inequalities states, “If a is greater than b, and b is greater than c, then a is greater than c. Similarly, if a is less than b, and b is less than c, then a is less than c”.
- If a > b and b > c, then a > c
- If a < b and b < c, then a < c
Representation of Inequalities Graphically
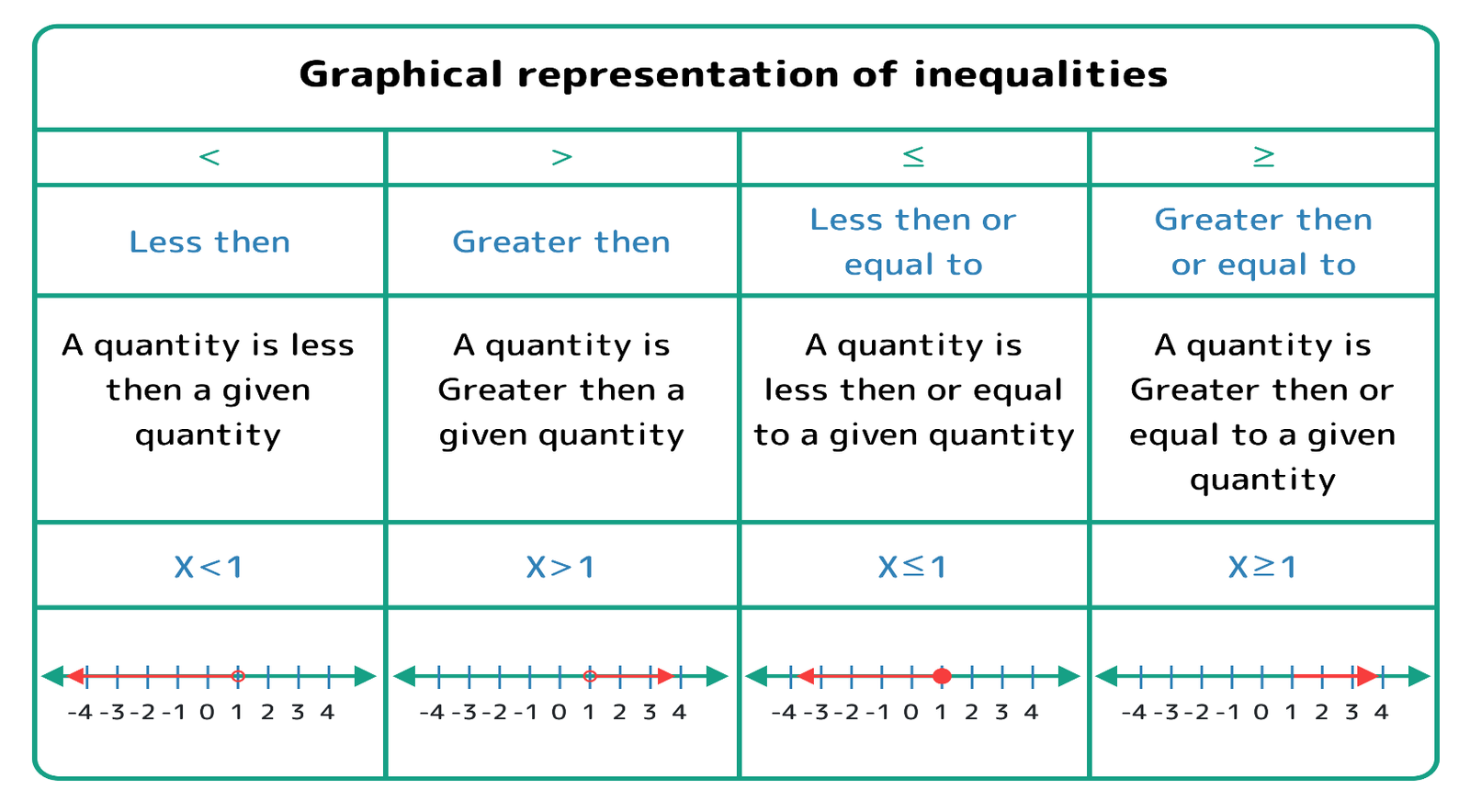
An empty circle (â—‹) represents that the limit value is not included in the solution set. A filled circle (â—) indicates that the solution set includes the limit value. An arrow pointing towards the right (→) for "greater than" or towards the left (←) for "less than" shows all possible values for the variable beyond the filled circle.
Solved Examples of inequality
Example 1
Solve the following inequality
3x + 7 > 16
Solution
Isolate the variable x on one side of the inequality sign to solve this inequality.
Step 1: Subtract 7 from both sides to get rid of the constant term on the left side.
3x +7 – 7 > 16 - 7
3x > 9
Step 2: Divide both sides by 3 to solve for x.
3x/3 > 9/3
x > 3
So the solution to the inequality is x > 3.
Example 2:
Solve the following inequality
-7 < 3x + 5 < 6
Solution
Break it down into two separate inequalities and solve them systematically.
Step 2: Solve the left inequality 7 < 3x + 5
Isolate 3x on one side by subtracting 5 from all parts of the inequality.
-7 - 5 < 3x + 5 - 5
-12 < 3x
Divide both sides by 3 to solve for x.
-12/3 < 3x/3
-4 < x
The solution to the left inequality is x > -4.
Step 2: Solve the right inequality 3x + 5 < 6
To isolate 3x on one side by subtracting 5 from all parts of the inequality:
3x + 5 - 5 < 6 - 5
3x < 1
Divide both sides by 3 to solve for x. The inequality sign remains the same because we are dividing by a positive number.
3x/3 < 1/3
x < 1/3
The solution to the right inequality is x < 1/3.
Step 3: Combine the individual solutions.
Solution set = {-4 < x < 1/3}
Conclusion
We explored the concept of inequality in this article. We have discussed its types with examples. We described all the important properties of inequity. We did different examples of inequality to learn how to solve inequality problems.
