To calculate result you have to disable your ad blocker first.

Interval in Mathematics: Definition, Types, and Examples

Publish Date: 03 Oct, 2023
Table of Content
Interval provides a concise way to represent a range of values along the real number line without having to list each number. It consists of all real numbers between two specified values. This concept of intervals plays a pivotal role in calculus, algebra, and statistics.
The focus of this article is a thorough exploration of intervals, including an analysis of their various types and the solution of example problems to solidify this concept.
What is an Interval?
An interval in mathematics is defined as a set of real numbers that includes all numbers between any two specified numbers of the set R. These two specified numbers are typically referred to as the endpoints or bounds of the interval.
For example, all real numbers between 6 to 10 is an interval.
Intervals can be represented using inequalities. The inequalities 2 ≤ x ≤ 5 can be represented as the closed interval [2, 5], including both 2 and 5.
Types of Intervals
Intervals can be classified based on their endpoint. Here are some most common types of intervals in mathematics:
- Closed Intervals
- Open Intervals
- Half-open or Half-Closed Interval
- Degenerated Intervals
- Bounded and Unbounded Intervals
Closed Interval [a, b]
A closed interval includes both endpoints, a and b, along with all the numbers in between. For example, [2, 5] represents the closed interval from 2 to 5, including both 2 and 5.
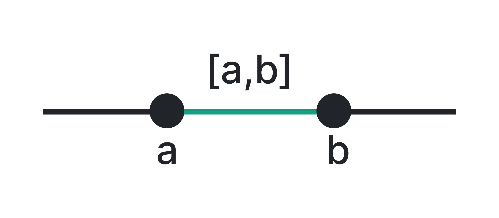
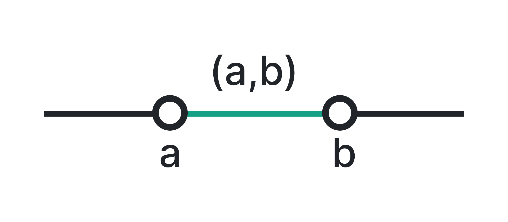
Open Interval (a, b)
An open interval includes all the numbers between a and b but excludes the endpoints. It is represented using parentheses. For instance, (1, 4) denotes the open interval from 1 to 4, excluding 1 and 4.
Half-open or Half-Closed Interval
This type of interval includes one endpoint and excludes the other. It can be either left or right closed. An example of a left closed interval is [a, b), where a is included and b is excluded. A right-closed interval is represented as (a, b], where a is excluded and b is included.
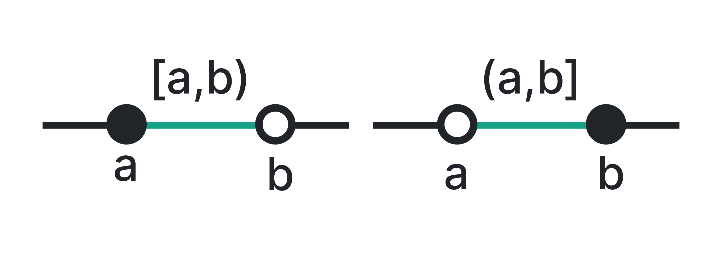
Degenerate Intervals
A degenerate interval consists of a single value. For example, the interval [a, a] consists only of the point a.
Bounded and Unbounded Intervals
A bounded interval has finite endpoints, like [a, b] where a and b are real numbers. An unbounded interval has one or both endpoints that extend infinitely, like (a, ∞) or (-∞, b).
Here is a table summarizing the different types of intervals with inequalities and their notations:
Interval Type | Interval Notation | Inequality Representation | Description |
Open Interval | (a, b) | a < x < b | All real numbers x such that a < x < b. |
Degenerate Interval | [a, a] = {a} | a = x | An interval containing only a single value. |
Closed Interval | [a, b] | a ≤ x ≤ b | All real numbers x such that a ≤ x ≤ b. |
Empty Interval | [b, a] = (b, a) = [b, a) = (b, a] = (a, a) = [a, a) = (a, a] = { } = Φ | Not applicable (No numbers in the interval) | An interval with no numbers between a and b. |
Left-Closed, Right-Open Interval | [a, b) | a ≤ x < b | All real numbers x such that a ≤ x < b. |
Left-open, Right-Closed Interval | (a, b] | a < x ≤ b | All real numbers x such that a < x ≤ b. |
Left-bounded, Open, and Right-Unbounded | (a, +∞) | x > a | All real numbers x such that x > a. |
Left-bounded, Closed, and Right-Unbounded | [a, +∞) | x ≥ a | All real numbers x such that x ≥ a. |
Left-Unbounded and Right-Bounded, Open | (-∞, b) | x < b | All real numbers x such that x < b. |
Left-Unbounded and Right-Bounded, Closed | (-∞, b] | x ≤ b | All real numbers x such that x ≤ b. |
Unbounded Interval at Both Ends | (-∞, +∞) or [-∞, +∞] = R | Not applicable (Covers all real numbers) | The set of all real numbers, covering the entire real number line. |
Common Properties of Interval
Here are some of the most significant properties of intervals:
- The union of any collection (finite or infinite) of intervals can also be an interval or a union of intervals.
- The complement of an interval is the set of real numbers that do not belong to the interval.
- The intersection of two intervals is the set of real numbers that are contained in both intervals.
- The distance between the endpoints of an interval is its length.
- If one interval is entirely contained within another, it is said to be a subset.
Importance of Interval in Mathematics
Intervals are of great importance in mathematics for several reasons:
Representation of Sets of Numbers: Intervals provide a concise and efficient way to represent sets of real numbers. They allow mathematicians to describe continuous ranges of values with simplicity and precision. This representation is especially useful in calculus, real analysis, and solving inequalities.
Probability and Statistics: In probability and statistics, intervals are used to represent confidence intervals, prediction intervals, and tolerance intervals. These intervals help quantify uncertainty and make probabilistic statements about data.
Function Domains and Ranges: The domains and ranges of functions are determined using intervals. They help determine where a function is defined and where it takes on specific values. This is crucial for understanding the behavior of functions and solving equations involving them.
Set Theory and Topology: Intervals are studied in set theory and topology, where they are used to define open sets, closed sets, and various types of topological spaces. These concepts are crucial in the study of continuity and convergence.
Solved Example of Intervals
Example 1:
A delivery service guarantees to deliver packages within 2 to 5 business days. How this delivery period can be expressed as an interval?
Solution: The delivery period can be represented as the closed interval [2, 5]. This interval signifies that the delivery service guarantees to deliver packages in 2, 3, 4, or 5 business days.
Example 2: An amusement park ride has a height restriction. Riders must be taller than 48 inches but no taller than 72 inches. Write this restriction in interval.
Solution:
The interval for this restriction can be written as (48, 72]
Conclusion
In this article, we have discussed the definition of interval with examples. We studied its different types. We examined common properties of intervals that are useful in mathematics. The importance of intervals has been covered in this blog. We solved some examples to illustrate this concept.
