To calculate result you have to disable your ad blocker first.

Integer Operations – Properties and Rules

Table of Content
Let’s understand the definition of integers before diving into the complexities of integer operations. Integers refer to whole numbers (without fractions) with positive, negative, or zero values. In mathematical terms, we represent integers as {..., -3, -2, -1, 0, 1, 2, 3, ...}.
Addition, subtraction, multiplication, and division are four basic arithmetic operations that can be performed on integers. Addition and subtraction are inverse actions that shift integers left or right on a number line. Multiplication is a way of expressing multiple additions in a simpler form. Multiplication and division are reciprocal functions.
Integers play a vital role in our daily lives. We encounter them everywhere – when shopping for groceries, keeping track of money, or checking the temperature. They truly surround us. In this article, we will delve into the world of integer operations, discussing their properties, rules, and applications. We'll also demonstrate how to perform various operations on integers using examples
Basic Integer Operations
Addition: The addition of integers involves combining two or more numbers to find their total. When dealing with positive numbers, addition is as straightforward as counting forwards. However, things get interesting when we introduce negative numbers.
Subtraction: The inverse of addition is subtraction, which involves finding the difference between two integers. It is crucial to grasp the concept of subtracting negatives and positives to perform accurate calculations.
Multiplication: Adding a number to itself multiple times is called multiplication. When dealing with integers, we need to consider the signs of the numbers being multiplied.
Division: The division is the process of sharing a quantity equally. However, division with integers requires attention to the signs of both the dividend and divisor.
Rules for Integer Operations
Addition and subtraction of integers
When adding integers with the same sign, we simply add their absolute values and keep the common sign.
For example: (+5) + (+3) = + 8 or (-5) + (-3) = - 8
When adding integers with different signs, we find the difference between their absolute values and keep the sign of the integer with the greater absolute value.
For example: (-9) + (+5) = - 4.
Subtracting integers can be rewritten as adding the additive inverse
For example: (+8) - (-3) can be rewritten as (+8) + (+3) = +11.
Multiplication and division of Integers
The product of two integers with the same sign is always positive while the product of two integers with different signs is always negative.
∴ (+6) × (+2) = +12 and (-6) × (+2) = -12.
The rule for dividing integers is the same as for multiplication. When two integers have the same sign, their quotient is always positive. The result of dividing two integers with different signs will always be negative.
∴ (+10) / (+2) = +5 and (-10) / (+2) = -5
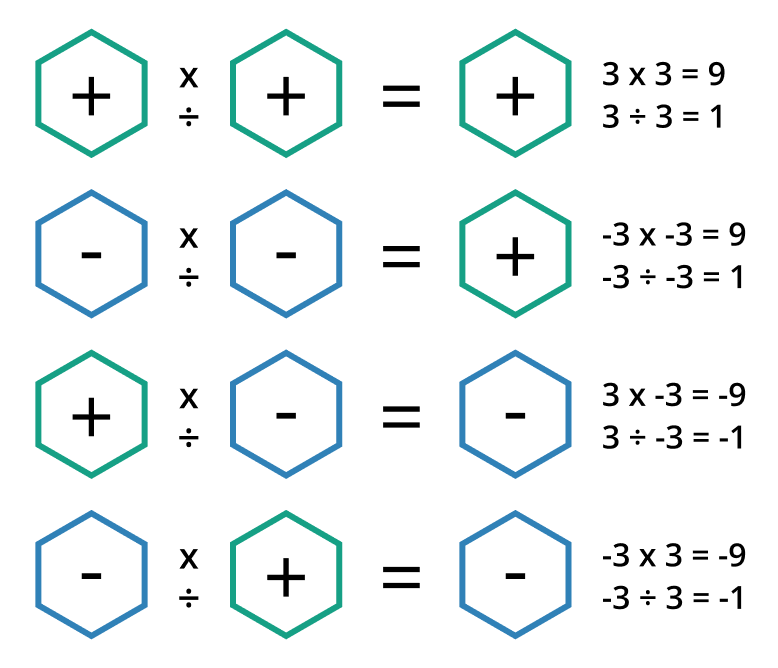
Order of Operations
We must follow the order of operations to perform multiple operations on integers. Depending on the region or curriculum, this is commonly referred to as PEMDAS (Parentheses, Exponents, Multiplication and Division, and Addition and Subtraction) or BODMAS (Brackets, Orders or powers and roots, Division and Multiplication, and Addition and Subtraction). According to this rule:
- First, evaluate expressions within parentheses or brackets.
- Then, tackle any exponents, powers, or orders.
- Next, carry out multiplication and division, moving from left to right.
- Finally, perform addition and subtraction, also from left to right.
Addition Properties of Integer
- Closure Property: The addition of two integers is always an integer.
If a, b ∈ Z, then (a + b) ∈ Z
- Commutative Property: The order of addition does not affect the result.
If a, b ∈ Z, then (a + b) = (b + a)
- Associative Property: The grouping of integers during addition does not affect the result.
If a, b, c ∈ Z, then (a + b) + c = a + (b + c).
- Identity Property: The sum of any integer and zero is the integer itself.
If a ∈ Z, then a + 0 = a.
- Inverse Property: Every integer has an additive inverse, which is another integer that, when added to the original integer, gives zero.
For any integer a, an integer b exists such that a + b = 0.
Subtraction Properties of Integers
- Closure Property: The subtraction of two integers is always an integer.
If a, b ∈ Z, then (a - b) ∈ Z
- Commutative property: The order of subtraction matters and changing the order of integers can result in different outcomes. If a, and b are integers. Then (a - b) is not necessarily equal to (b - a).
- Associative Property: Associative property does not hold in subtraction. If a, b, and c ∈ Z then (a - b) - c ≠ a - (b - c).
- Zero property of subtraction: Subtracting zero from any integer results in the same integer. If a is an integer, then a - 0 = a.
- Subtraction with the same integer: When subtracting an integer from itself, the result is always zero. If a is an integer, then a - a = 0.
Division Properties of Integers
- Closure Property: The division of two integers may or may not be an integer.
14, 7 ∈ Z, then 14 ÷ 7 = 2 ∈ Z.
17, - 8 ∈ Z, then 17 ÷ (- 8) = 17/-8 ∉ Z.
- Commutative Property: Commutative Property does not hold in division.
If a, b ∈ Z, then (a ÷ b) ≠ (b ÷ a)
- Division by Zero: It is undefined to divide any integer by zero (0). The result is not a valid numerical value. However, the result is always zero (0) when zero (0) is divided by any non-zero integer.
- Division by One: The answer will always be the same integer value when 1 divides an integer.
∴ a ÷ 1 = a.
The quotient is the additive inverse of the original integer when an integer is divided by -1.
∴ (a) ÷ (-1) equals -a.
Multiplicative Properties of Integer
- Closure and Commutative property: Closure and commutative property hold in multiplication.
- Associative Property: The grouping of integers during multiplying does not influence the result.
If a, b, c ∈ Z, then (a × b) × c = a × (b × c).
- Multiplicative Identity Property: The product of any integer and one is the integer itself.
If a ∈ Z, then a × 1 = a.
- Multiplicative Inverse Property: Every integer has a multiplicative inverse except 0. It is the reciprocal of the original integer.
For any integer a, there exists an integer 1/a, such that (a) (1/a) = 1.
Applying Integer Operations in Real-Life
Let’s explore some notable applications of integer operation in our daily life.
Banking Transactions
Integer operations play a significant role in managing finances. Bank accounts often involve positive and negative integers, representing deposits and withdrawals, respectively.
Temperature Changes
In weather forecasts, integer operations help in calculating temperature changes. Positive and negative integers denote temperature increases and decreases, respectively.
Elevations and Depths
In geography and surveying, integer operations are vital for representing elevations and depths. Positive integers indicate aboveground levels, while negative integers represent belowground levels.
Stock Market Trends
Integer operations are used to analyze stock market trends, where positive and negative integers represent gains and losses in stock
Solved Examples
Example 1
Students receive (+3) marks for every correct answer and (-1) marks for every incorrect answer in a quiz. Raju answered all the questions and scored 15 marks, even though he got 8 correct answers. Calculate how many answers Raju gave incorrectly.
Solution:
Step 1: Marks given for one correct answer = +3 marks.
Raju got 8 correct answers, so marks for 8 correct answers = 3 × 8 = 24 marks.
Step 2: Raju's score = 15 marks.
Marks obtained for incorrect answers = Raju's score - Marks for correct answers
Marks obtained for incorrect answers = 15 - 24 = -9 marks (negative because they are incorrect answers).
Step 3: Marks are given for one incorrect answer = -1 mark.
Number of incorrect answers = Marks obtained for incorrect answers ÷ Marks for one incorrect answer
Number of incorrect answers = (-9) ÷ (-1) = 9
Thus, Raju attempted 9 incorrect answers.
Example 2:
Simplify the following expression:
4 + 5 × (10 – 2)2 ÷ 2
Solution:
Step 1: Start by evaluating the expression inside the brackets.
10 – 2 = 8
Step 2: Next, calculate the square of the result from Step 1.
82 = 64
Step 3: Now, perform any division or multiplication from left to right.
5 × 64 = 320
Step 4: Lastly, perform any addition from left to right.
4 + 320 = 324
Therefore, the simplified result of the expression is:
4 + 5 × (10 – 2)2 ÷ 2 = 324
Conclusion
Integer operations are fundamental in mathematics, allowing us to manipulate whole numbers efficiently. You can enhance your mathematical skills and problem-solving abilities by understanding the properties, rules, and real-life applications of integer operations.
